KMP与字符串Hash

最近学习算法时，在KMP和字符哈希上遇到了一些困难。这篇笔记记录整理对于KMP与字符串哈希的一些个人理解，供自己复习使用。

---

KMP

模板题：给定一个字符串S，以及一个模式串P，所有字符串中只包含大小写英文字母以及阿拉伯数字。模式串P在字符串S中多次作为子串出现。
求出模式串P在字符串S中所有出现的位置的起始下标。

对于KMP这一个复杂的算法，个人认为在理解上有两个难点，一个是next数组的求解，另一个是利用next数组对于KMP算法的实现。

next 数组

• 假设有一个字符串s(下标从0开始)，那么它以i号位作为结尾的子串就是s[0:i]
  • 对于子串s,长度为k+1的前缀和后缀就是s[0:k]和s[i-k:i]

构造一个int数组next。其中，next[i]表示使子串s[0:i]中的前缀和后缀相等的最大的k，即满足s[0:k] == s[i-k:i]的最大的k。

• 相等的前缀和后缀不能是整个字符串，即k不能等于i
• 如果不存在这样的k，那么next[i] = -1
• next[i]就是所求最长相等前后缀中前缀的最后一个字符的下标

用递推求解 next 数组

递推求解，即已知next[0]~`next[i-1]，求解next[i]`。

• 如果s[next[i-1]+1] == s[i]，那么next[i] = next[i-1] + 1
• 否则，令k = next[i-1]，如果s[next[k]+1] == s[i]，那么next[i] = next[k] + 1，否则继续令k = next[k]，直到k = -1或者s[next[k]+1] == s[i]为止。

看一个例子：
现在让 s = “abababc”

1. 假设已经有了next[0]~next[3],求解next[4]

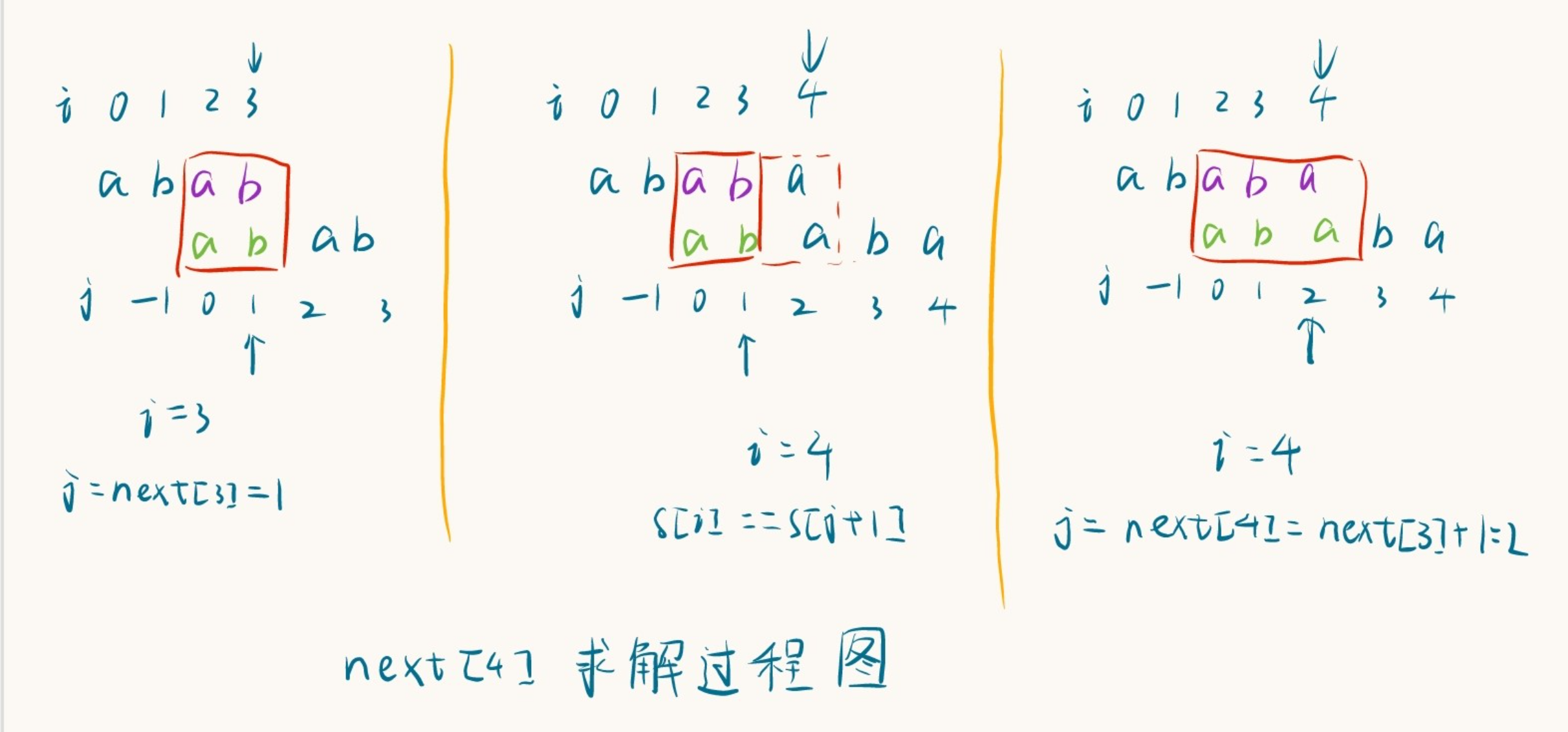
• 当已经得到 next[3] = 1 时，最长相等前后缀为 “ab”，之后计算 next[4] 时，由于 s[4] == s[next[3] + 1] (这里的为什么要用 next[3]？想想至尊概念)，因此可以把最长相等前后缀 “ab” 扩展为 “aba”，因此 next[4] = next[3] + 1，并令 j 指向 next[4]。

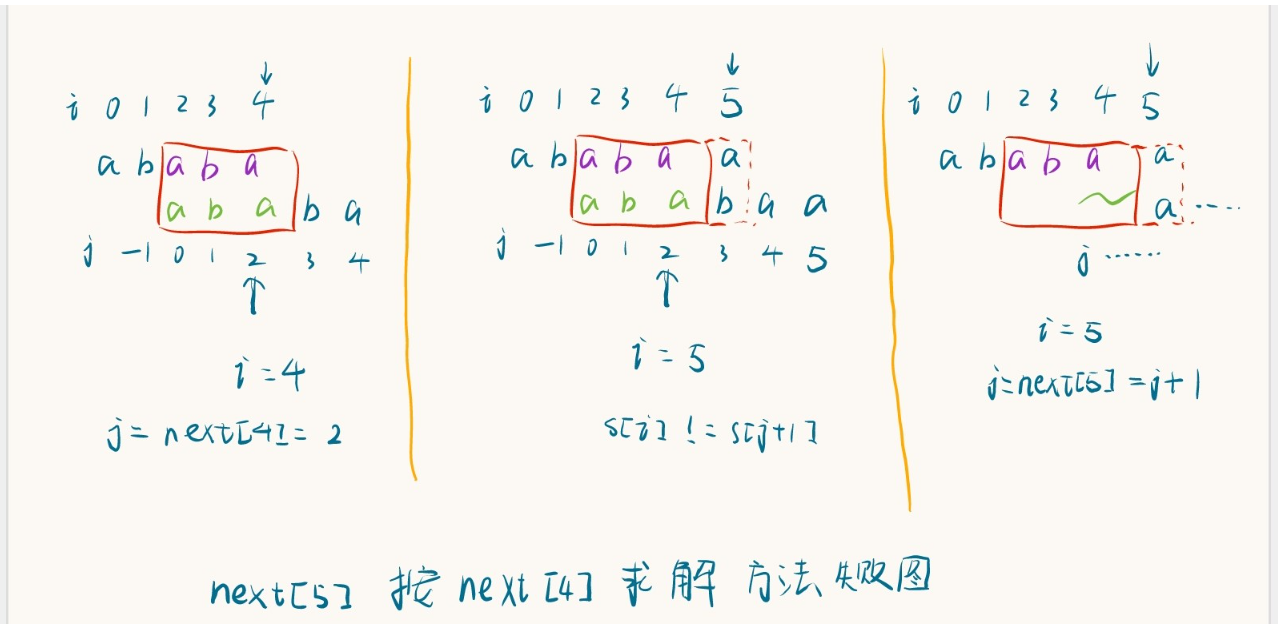
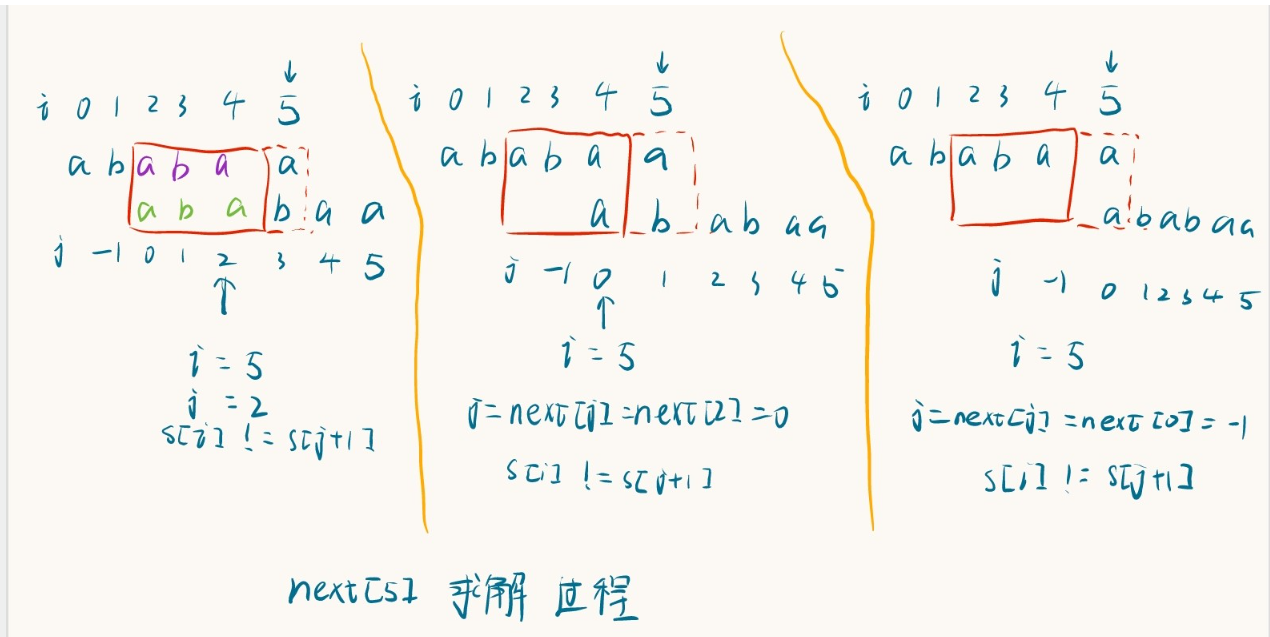
2. 假设已经有了next[0]~next[4],求解next[5]

next[0] = -1;
for (int i = 1, j = -1; i < len; i ++)// j 表示i-1号位的最长相等前后缀的前缀的最后一个字符的下标
{
    while (j != -1 && s[i] != s[j + 1]) // 前后缀匹配不成功
    {
        // 反复令 j 回退到 -1，或是 s[i] == s[j + 1]
        j = next[j];
    }
    if (s[i] == s[j + 1]) // 匹配成功
    {
        j ++; // 最长相等前后缀变长
    }
    next[i] = j; // 令 next[i] = j
}   

认识KMP

从一个例子开始，让 s = “abababaabc”, p = “ababaab”

• 令 i 指向 text 的当前欲比较位，令 j 指向 pattern 中当前已被匹配的最后位
  • 这样只要 text[i] == pattern[j + 1] 成立，就说明 pattern[j + 1] 也被成功匹配
• 直到 j 达到 m - 1(m 为 pattern 长度) 时说明 pattern 是 text 的子串

下面是p[3+1]与s[4]匹配成功的情况：

下面是p[4+1]与s[5]匹配失败后KMP的处理：

Remark: KMP的核心就是当匹配失败或者匹配完整个Pattern子串后，将j=-1从头遍历改为j=next[j],减少时间上的开销

for (int i = 0, j = -1; i < m; i ++)
    {
       while (j != -1 && s[i] != p[j + 1])
       {
           j = ne[j];
       }
       if (s[i] == p[j + 1])
       {
           j ++; // 匹配成功时，模板串指向下一位
       }
       if (j == n - 1) // 模板串匹配完成，第一个匹配字符下标为 0，故到 n - 1
       {
           // 匹配成功时，文本串结束位置减去模式串长度即为起始位置
           cout << i - j << ' ';
           // 模板串在模式串中出现的位置可能是重叠的
           // 需要让 j 回退到一定位置，再让 i 加 1 继续进行比较
           // 回退到 ne[j] 可以保证 j 最大，即已经成功匹配的部分最长
           j = ne[j]; 
       }
    }

KMP的时间复杂度

结论：KMP的时间复杂度为 $O(m+n)$
首先在整个for循环中，step=1，所以i的变化次数是 $O(m)$ ，考虑j的变化次数，j最多增加m次或者减少m次，所以j的变化次数也是 $O(m)$。
考虑到计算next数组需要 $O(n)$的复杂度，所以整个算法的时间复杂度为 $O(m+n)$ 。

---

字符串Hash

什么是字符串哈希

字符串哈希就是将字符串映射到一个整数上，这个整数就是字符串的哈希值。

• 把字符串看成是一个 P 进制数，每个字符的 ASCII 码对应数的一位
  • 经验上将P取131或13331，避免冲突（字符串哈希不考虑冲突的问题）
• 字符串很长，对应的数太大，通过 $mod(2^{64})$ 把它映射到 $[0,2^{64}-1]$
• 用 unsigned long long 存储，溢出相当于对 2^64 取模，省略了手动运算

具体实现

unsigned long long h[N], p[N]; // h[i]存储字符串前i个字母的哈希值, p[i]存储 P^i

void hash_init(char str[], int len)
{
    p[0] = 1;
    for (int i = 1; i <= len; i ++ )
    {
        h[i] = h[i - 1] * P + str[i];
        p[i] = p[i - 1] * P;
    }
}

unsigned long long get(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}