信号与系统期中Review
Signal and System 期中Review
Chapter 0
(1) Preknowledge
- $z=Re{z}+j*Im{z}$
- $z=|z|e^{j\theta}$
- $z^*=|z|e^{-j\theta }=Rez-j*Imz$
- $\displaystyle \cos \theta=\frac{e^{j\theta} +e^{-j\theta}}{2}$
- $\displaystyle \sin \theta=\frac{e^{j\theta} -e^{-j\theta}}{2j}$
- $\displaystyle \sum_{n=0}^{\infty}(z_0)^n=\frac{1}{1-z_0}$ iff $|z_0|<1$
Chapter 1
(1) Energy and Power
- For any signal $x(t)$ or $x[n]$, we can define its total energy as:
$$E=\int_{-\infty}^{\infty}|x(t)|^2dt$$
$$E=\sum_{n=-\infty}^{\infty}|x[n]|^2$$
- The average power is defined as:
$$P=\frac{E}{t_2-t_1}$$
$$P=\frac{E}{n_2-n_1+1}$$
- Over infinite time interval
- Continuous:$E_{\infty}=\lim_{T \to \infty}\int_{-T}^{T}|x(t)|^2dt = \int_\infty^\infty |x(t)|^2dt$
- Discrete:$E_{\infty}=\lim_{N \to \infty}\sum_{n=-N}^{N}|x[n]|^2 = \sum_{n=-\infty}^\infty |x[n]|^2$
- $P=\lim_{T \to \infty}\frac{1}{2T}\int_{-T}^{T}|x(t)|^2dt$
- $P=\lim_{N \to \infty}\frac{1}{2N+1}\sum_{n=-N}^{N}|x[n]|^2$
3.
- Finite energe signals: $E<\infty$,$P=0$
- Finite power signals: $P<\infty$,$E=\infty$
- Infinite energy signals: $E=\infty$
- Infinite power signals: $P=\infty$
(2) Unit Impulse Function and Unit Step Function
Unit impulse is defined as:
$\delta[n]=\begin{cases}
0, & n=1\
1, & n=0
\end{cases}$
$\delta(t)=\begin{cases}
0, & t=1\
1, & t=0
\end{cases}$Unit step is defined as:
$u[n]=\begin{cases}
0, & n<0\
1, & n> 0
\end{cases}$
$u(t)=\begin{cases}
0, & t<0\
1, & t> 0
\end{cases}$Sampling property
- $x[n]\delta[n-n_0]=x[n_0]\delta[n-n_0]$
- $x(t)\delta(t-t_0)=x(t_0)\delta(t-t_0)$
(3) Basic System Properties
- With Memory:Output depends on current and previous inputs
- Invertible:If $x_1(t)=x_2(t)$,then $y_1(t)=y_2(t)$
- Causal:Output depends on inputs at the present and past time
- Stable:If $|x(t)|<\infty$,then $|y(t)|<\infty$
- Time Invariant:a time shift in the input signal causes the same time shift in the output signal
- Check $f({x(t-t_0)})$(which only do the change on t) is equal to $y(t-t_0)$(which do the change on $t-t_0$)
- Linearity: $f(ax_1(t)+bx_2(t))=ay_1(t)+by_2(t)$
Chapter 2
(1) Linear Time Invariant(LTI) Systems
- Impulse response: $h(t)=f(\delta(t))$
(2) Properties of LTI Systems
- Commutative: $x(t)*h(t)=h(t)*x(t)$
- Associative: $x(t)*[h_1(t)*h_2(t)]=[x(t)*h_1(t)]*h_2(t)$
- Distributive: $x(t)*[h_1(t)+h_2(t)]=x(t)*h_1(t)+x(t)*h_2(t)$
- Without Memory:
- $h[n]=0$ for $n\neq 0$
- $h(t)=0$ for $t\neq 0$
- Invertibility: $h_0(t)*h_1(t)=\delta(t)$ then, the system with impulse response $h_1(t)$ is the inverse of the system with impulse response $h_0(t)$
- Causality: $h(t)=0$ for $t<0$
- Equivalent to the condition of initial rest: if $t\le t_0,x(t)=0$, then $y(t_0)=0 $
- Stability: Absolutely summable/absolutely integrable
- $\int_{-\infty}^{\infty}|h(\tau)|d\tau<\infty$
- $h[n]=\sum_{n=-\infty}^{\infty}|h[n]|<\infty$
Chapter 3
(1) The response of LTI systems to complex exponential signals
- Let $x(t)=e^{st}$
- $y(t)=H(s)e^{st}$, where $H(s)=\int_{-\infty}^{\infty}h(\tau)e^{-s\tau}d\tau$
- $e^{st}$ is an eigenfunction of LTI system and $H(s)$ is the corresponding eigenvalue
- Let $x[n]=z^n$
- $y[n]=H(z)z^n$, where $H(z)=\sum_{n=-\infty}^{\infty}h[n]z^{-n}$
- $z^n$ is an eigenfunction of LTI system and $H(z)$ is the corresponding eigenvalue
(2) Fourier series representation of periodic signals
- Continuous-time periodic signals
- $x(t)=\sum_{k=-\infty}^{\infty}a_ke^{jk\omega_0t}$ —Synthesis equation
- $a_k=\frac{1}{T_0}\int_{T_0}x(t)e^{-jk\omega_0t}dt$ —Analysis equation
- $T_0$ is the period of $x(t)$
- $\omega_0=\frac{2\pi}{T_0}$
e.g. The square wave
Conclusion: $\displaystyle a_k=\frac{2T_1}{T}\frac{\sin (k\omega_0 T_1)}{k\omega_0T_1}=\frac{\sin (k\omega_0T_1)}{k\pi},k\neq 0$
(3) Convergence of Fourier series
- Finite energy condition: $\displaystyle \int_{-\infty}^{\infty}|x(t)|^2dt<\infty$
- Dirichlet conditions:
- $x(t)$ is absolutely integrable over any finite interval
- $x(t)$ has a finite number of maxima and minima in any finite interval
- $x(t)$ has a finite number of discontinuities in any finite interval
(4) Properties of Fourier series
- Linearity:
- $x(t)\stackrel{FS}{\longleftrightarrow} a_k$, $y(t)\stackrel{FS}{\longleftrightarrow} b_k \Rightarrow ax(t)+by(t)\stackrel{FS}{\longleftrightarrow} Aa_k+Bb_k$
- Time shifting:
- $x(t)\stackrel{FS}{\longleftrightarrow} a_k \Rightarrow y(t)=x(t-t_0)\stackrel{FS}{\longleftrightarrow} a_ke^{-jk\omega_0t_0}$
- Time reversal:
- $x(t)\stackrel{FS}{\longleftrightarrow} a_k \Rightarrow y(t)=x(-t)\stackrel{FS}{\longleftrightarrow} a_{-k}$
- Time scaling:
- $x(t)\stackrel{FS}{\longleftrightarrow} a_k \Rightarrow y(t)=x(at)\stackrel{FS}{\longleftrightarrow} a_k$
- Multiplication:
- $x(t)\stackrel{FS}{\longleftrightarrow} a_k$, $y(t)\stackrel{FS}{\longleftrightarrow} b_k \Rightarrow z(t)=x(t)y(t)\stackrel{FS}{\longleftrightarrow}\sum_{l=-\infty}^\infty a_lb_{k-l}$
- Conjugation and conjugate symmetry:
- $x(t)\stackrel{FS}{\longleftrightarrow} a_k \Rightarrow x^*(t)\stackrel{FS}{\longleftrightarrow} a_{-k}^*$
- If $x(t)$ is real, then $a_k=a_{-k}^*$
- If $x(t)$ is real and even, then $a_k$ is real and even
- If $x(t)$ is real and odd, then $a_k$ is imaginary and odd
- Differentiation:
- $x(t)\stackrel{FS}{\longleftrightarrow} a_k \Rightarrow y(t)=\frac{dx(t)}{dt}\stackrel{FS}{\longleftrightarrow} jk\omega_0a_k$
- Integration:
- $x(t)\stackrel{FS}{\longleftrightarrow} a_k \Rightarrow y(t)=\int_{-\infty}^tx(\tau)d\tau\stackrel{FS}{\longleftrightarrow} \frac{a_k}{jk\omega_0}$
- Frequency shifting:
- $x(t)\stackrel{FS}{\longleftrightarrow} a_k \Rightarrow y(t)=x(t)e^{jM\omega_0t}\stackrel{FS}{\longleftrightarrow} a_{k-M}$
- Periodic convolution:
- $x(t)\stackrel{FS}{\longleftrightarrow} a_k$, $y(t)\stackrel{FS}{\longleftrightarrow} b_k \Rightarrow z(t)=x(t)*y(t)\stackrel{FS}{\longleftrightarrow} Ta_kb_k$
- Parseval’s theorem:
- $\displaystyle \sum_{k=-\infty}^{\infty}|a_k|^2=\frac{1}{T}\int_{T}|x(t)|^2dt$
(5) Fourier series for discrete-time periodic signals
- $x[n]=\sum_{k=-\infty}^{\infty}a_ke^{jk\omega_0n}$ —Synthesis equation
- $a_k=\frac{1}{N}\sum_{n=0}^{N-1}x[n]e^{-jk\omega_0n}$ —Analysis equation
- $a_k$ is periodic with period $N$,that is, $a_k=a_{k+rN}$
e.g. The square wave for discrete-time
$\displaystyle a_k=\frac{\sin(\pi k)}{N\sin(\frac{\pi}{N}k)}$ when $k\neq 0,\pm kN$
$\displaystyle a_k= \frac{2N_1+1}{N}$ when $k=0,\pm kN$
Properties
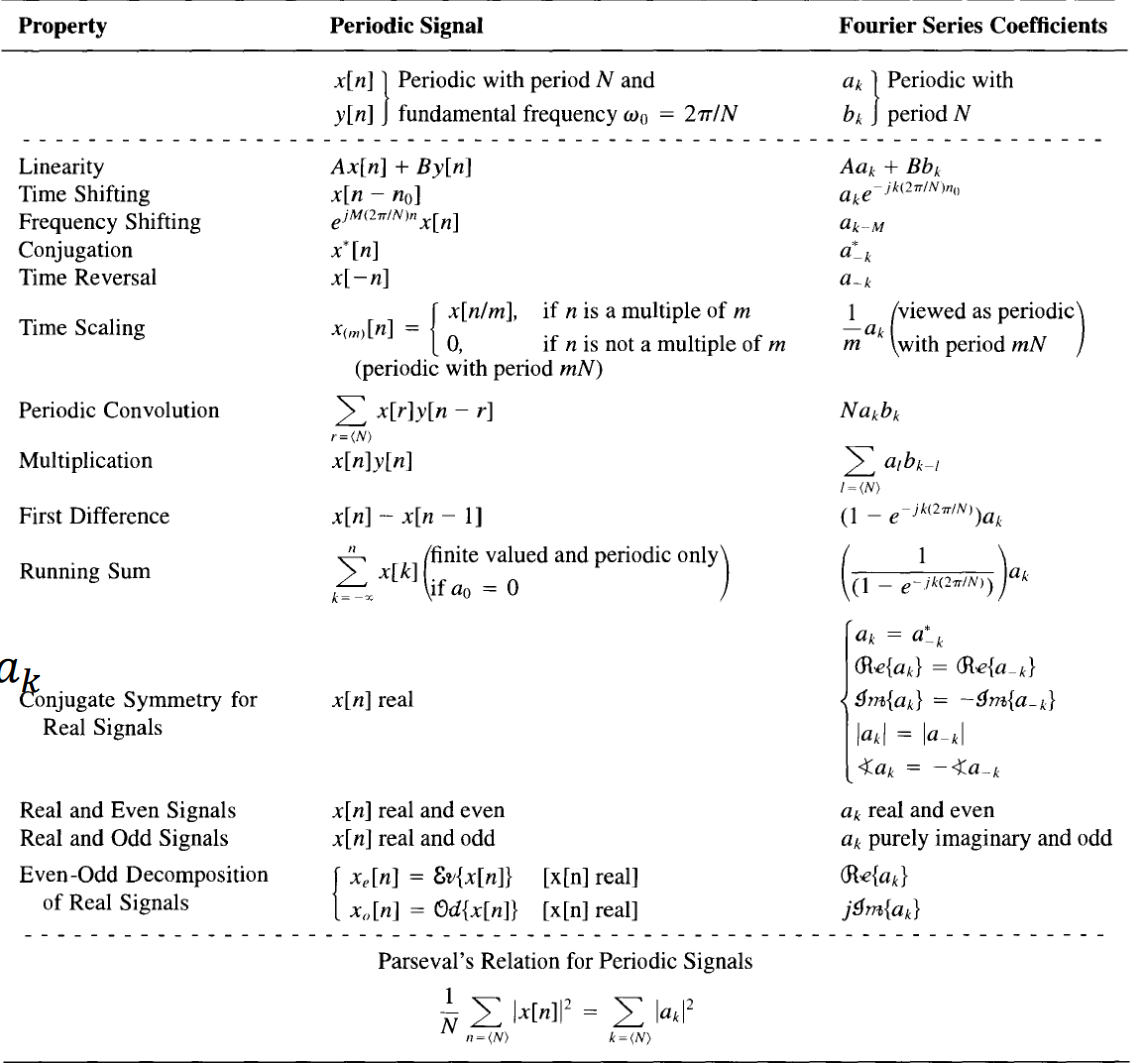
(6) Fourier series and LTI systems
- CT system
- $H(s) = \int_{-\infty}^{\infty}h(\tau)e^{-s\tau}d\tau \Rightarrow H(j\omega)=\int_{-\infty}^{\infty}h(\tau)e^{-j\omega\tau}d\tau$
- $e^{j\omega t}\to H(j\omega)e^{j\omega t}$
Conclusion: $b_k=a_kH(j\omega_0)$
- DT system
- $H(z) = \sum_{n=-\infty}^{\infty}h[n]z^{-n} \Rightarrow H(e^{j\omega})=\sum_{n=-\infty}^{\infty}h[n]e^{-j\omega n}$
- $z^n\to H(e^{j\omega})z^n$
Conclusion: $b_k=a_kH(e^{j\omega_0})$
Chapter 4
(1) Fourier transform and Inverse Fourier transform
- $\displaystyle X(j\omega)=\int_{-\infty}^{\infty}x(t)e^{-j\omega t}dt$
- $\displaystyle x(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(j\omega)e^{j\omega t}d\omega$
- Convergence of FT: The same as Fourier series.
Regular Fourier Transform:
- $x_1(t)=\delta(t)\to X_1(j\omega)=1$
- $x_2(t)=1\to X_2(j\omega)=2\pi\delta(\omega)$
- $x(t)=e^{-at}u(t),a>0\to X(j\omega)=\frac{1}{a+j\omega}$
- $x(t)=e^{-a|t|},a>0\to X(j\omega)=\frac{2a}{\omega^2+a^2}$
- $\displaystyle x(t)=\begin{cases}
1,|t|<T_1\
0,|t|>T_1
\end{cases}\to X(j\omega)=\int_{T_1}^{T_1}e^{-j\omega t}dt=\frac{2\sin \omega T_1}{\omega}$ - $\displaystyle X(j\omega)=\begin{cases}
1,|\omega|<W \
0,|\omega|>W
\end{cases}\to x(t)=\frac{W}{\pi}\frac{\sin Wt}{Wt}$
- A periodic signal can be represented by a FS, but also a FT
- x(t) = $\displaystyle \sum_{k=-\infty}^{\infty}a_ke^{jk\omega_0t} \to X(j\omega)=2\pi\sum_{k=-\infty}^{\infty}a_k\delta(\omega-k\omega_0)$
Regular FT for periodic signals
- $x(t)=\sin \omega_0 t \to X(j\omega)=\frac{\pi}{j}[\delta(\omega-\omega_0)-\delta(\omega+\omega_0)]$
- $x(t)=\cos \omega_0 t \to X(j\omega)=\pi[\delta(\omega-\omega_0)+\delta(\omega+\omega_0)]$
(2) Properties of Fourier transform
- Linearity:
- $x(t)\stackrel{FT}{\longleftrightarrow} X(j\omega)$, $y(t)\stackrel{FT}{\longleftrightarrow} Y(j\omega) \Rightarrow ax(t)+by(t)\stackrel{FT}{\longleftrightarrow} aX(j\omega)+bY(j\omega)$
- Time shifting:
- $x(t)\stackrel{FT}{\longleftrightarrow} X(j\omega) \Rightarrow y(t)=x(t-t_0)\stackrel{FT}{\longleftrightarrow} X(j\omega)e^{-j\omega t_0}$
- Time reversal:
- $x(t)\stackrel{FT}{\longleftrightarrow} X(j\omega) \Rightarrow y(t)=x(-t)\stackrel{FT}{\longleftrightarrow} X(-j\omega)$
- Conjugation and Conjugate Symmetry
- $x(t)\stackrel{FT}{\longleftrightarrow} X(j\omega) \Rightarrow x^*(t)\stackrel{FT}{\longleftrightarrow} X^*(-j\omega)$
- If $x(t)$ is real, then $X(-j\omega)=X^*(j\omega)$
- If $x(t)$ is real and even, then $X(j\omega)$ is real and even
- If $x(t)$ is real and odd, then $X(j\omega)$ is imaginary and odd
- If $x(t)$ is imaginary and even, then $X(j\omega)$ is imaginary and even
- If $x(t)$ is imaginary and odd, then $X(j\omega)$ is real and odd
- $x(t)\stackrel{FT}{\longleftrightarrow} X(j\omega) \Rightarrow x^*(t)\stackrel{FT}{\longleftrightarrow} X^*(-j\omega)$
- Differentiation:
- $x(t)\stackrel{FT}{\longleftrightarrow} X(j\omega) \Rightarrow y(t)=\frac{dx(t)}{dt}\stackrel{FT}{\longleftrightarrow} j\omega X(j\omega)$
- Integration:
- $x(t)\stackrel{FT}{\longleftrightarrow} X(j\omega) \Rightarrow y(t)=\int_{-\infty}^tx(\tau)d\tau\stackrel{FT}{\longleftrightarrow} \frac{X(j\omega)}{j\omega}+\pi X(0)\delta(\omega)$
- $F(u(t))=\frac{1}{j\omega}+\pi\delta(\omega)$
- $x(t)\stackrel{FT}{\longleftrightarrow} X(j\omega) \Rightarrow y(t)=\int_{-\infty}^tx(\tau)d\tau\stackrel{FT}{\longleftrightarrow} \frac{X(j\omega)}{j\omega}+\pi X(0)\delta(\omega)$
- Time and frequency scaling:
- $x(t)\stackrel{FT}{\longleftrightarrow} X(j\omega) \Rightarrow y(t)=x(at)\stackrel{FT}{\longleftrightarrow} \frac{1}{|a|}X(\frac{j\omega}{a})$
- Duality:
- $x(t)\stackrel{FT}{\longleftrightarrow} X(j\omega) \Rightarrow X(t)\stackrel{FT}{\longleftrightarrow} 2\pi x(-j\omega)$
- 括号内 $j\omega$ 与t互换,括号外 $\omega$ 与t互换
- Other Properties
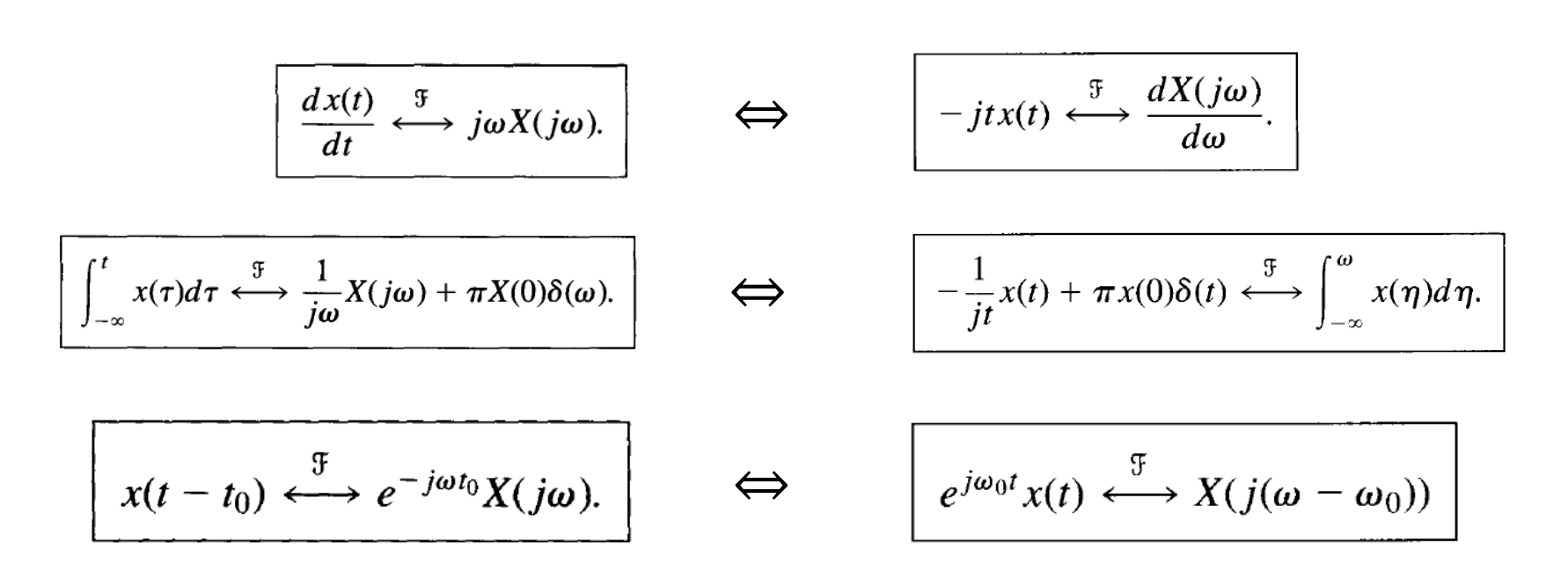
- $x(t)\stackrel{FT}{\longleftrightarrow} X(j\omega) \Rightarrow X(t)\stackrel{FT}{\longleftrightarrow} 2\pi x(-j\omega)$
- Parseval’s relation
- $\displaystyle \int_{-\infty}^{\infty}|x(t)|^2dt=\frac{1}{2\pi}\int_{-\infty}^{\infty}|X(j\omega)|^2d\omega$
- Convolution Properties
- $y(t)=x(t)*h(t)\stackrel{FT}{\longleftrightarrow} X(j\omega)H(j\omega)$
- Only stable system have $H(j\omega)$
- $y(t)=x(t)*h(t)\stackrel{FT}{\longleftrightarrow} X(j\omega)H(j\omega)$
- Multiplication Properties
- $y(t)=x(t)h(t)\stackrel{FT}{\longleftrightarrow} \frac{1}{2\pi}X(j\omega)*H(j\omega)$
(3) System characterized by LTI differential equations
$\displaystyle \sum_{k=0}^N a_k \frac{d^ky(t)}{dt^k}=\sum_{k=0}^Mb_k\frac{d^kx(t)}{dt^k}$
$\Rightarrow\displaystyle H(j\omega)=\frac{Y(j\omega)}{X(j\omega)}=\frac{\sum_{k=0}^Mb_k(j\omega)^k}{\sum_{k=0}^Na_k(j\omega)^k}$