信号与系统期末Review

Signal and System 期末Review

Chapter 5 The Discrete-Time Fourier Transform

Fourier Transform for Aperiodic Signals

1. • Discrete Fourier Transform: $x[n] = \displaystyle \sum_{k=-\infty}^{\infty} x[n]e^{-j\omega n}$
   • Inverse Fourier Transform: $x[n] = \displaystyle \frac{1}{2\pi}\int_{2\pi}X(\omega)e^{j\omega n}d\omega$
     • $X(e^{j\omega})(d\omega)/2\pi$ is the weight of different frequency

Note: $X(e^{j\omega})$ is a periodic function with period $2\pi$
Comparied with continuous FT: $e^{-j(\omega +2\pi)t }\neq e^{-j\omega}$ because t is not a integer.

2. Some DFT pairs
   • $x[n] = \delta[n] \leftrightarrow X(e^{j\omega}) = 1$
   • $x[n]=u[n] \leftrightarrow X(e^{j\omega}) = \frac{1}{1-e^{-j\omega}}+\pi \sum_{k=-\infty}^{\infty}\delta(\omega - 2\pi k)$
   • $x[n] = \alpha ^nu[n], |\alpha|<1 \leftrightarrow X(e^{j\omega}) =\frac{1}{1-\alpha e^{-j\omega}}$
   • $x[n] = \alpha^{|n|}, |\alpha|<1 \leftrightarrow X(e^{j\omega}) = \frac{1-\alpha^2}{1-2\alpha cos\omega + \alpha^2}$
   • $x[n]=\begin{cases}
     1, |n|\le N_1 \
     0, n>N_1
     \end{cases}\leftrightarrow X(e^{j\omega}) = \displaystyle \frac{sin[\omega (N_1+\frac{1}{2})]}{sin(\frac{\omega}{2})}$
   • $\displaystyle x[n]=\frac{\sin \omega _0n}{\pi n}\leftrightarrow X(e^{j\omega}) = \begin{cases}
     1, |\omega|<\omega _0 \
     0, |\omega|>\omega _0\end{cases}$
3. Convergence of DFT:
   • Absolutely summable: $\displaystyle \sum_{n=-\infty}^{\infty}|x[n]|<\infty$
   • Finite energy condition: $\displaystyle \sum_{n=-\infty}^{\infty}|x[n]|^2<\infty$

Fourier Transform for Periodic Signals

• $x[n] = \sum_{k=}a_ke^{jk(\frac{2\pi}{N})n}$
• $X(e^{j\omega}) = \displaystyle \sum_{k=-\infty}^{\infty}2\pi a_k\delta(\omega - k\frac{2\pi}{N})$

Properties of the Discrete-Time Fourier Transform

1. Periodicity : $X(e^{j(\omega +2\pi)}) = X(e^{j\omega})$
2. Linearity : $a_1x_1[n]+a_2x_2[n] \leftrightarrow a_1X_1(e^{j\omega})+a_2X_2(e^{j\omega})$
3. Time Shifting : $x[n-n_0] \leftrightarrow e^{-j\omega n_0}X(e^{j\omega})$
   • e.g. $X(e^{j\omega})=e^{j\omega}\leftrightarrow x[n] = \delta[n-1]$
4. Frequency Shifting : $e^{j\omega_0n}x[n] \leftrightarrow X(e^{j(\omega-\omega_0)})$
5. Conjugation : $x^*[n] \leftrightarrow X^*(e^{-j\omega})$
   • If $x[n]$ is real, $X(e^{j\omega}) = X^*(e^{-j\omega})$
     • Magnitude of $X(e^{j\omega})$ is even, phase of $X(e^{j\omega})$ is odd
6. Time Reversal : $x[-n] \leftrightarrow X(e^{-j\omega})$
   • x[n] even, $X(e^{j\omega})$ is even
   • x[n] odd, $X(e^{j\omega})$ is odd
   • x[n] read and even, $X(e^{j\omega})$ is real and even
   • x[n] read and odd, $X(e^{j\omega})$ is imaginary and odd
7. Difference : $x[n]-x[n-1] \leftrightarrow (1-e^{-j\omega})X(e^{j\omega})$
8. Accumulation: $\displaystyle \sum_{k=-\infty}^{n}x[k] \leftrightarrow \frac{1}{1-e^{-j\omega}}X(e^{j\omega})+\pi X(e^{j0})\sum_{k=-\infty}^{\infty}\delta(\omega - 2\pi k)$
9. Time expansion : $x_{(k)}[n]\leftrightarrow X(e^{j\omega k})$
   • $x_{(k)}[n] = \begin{cases}
     x[\frac{n}{k}], n = 0, \pm k, \pm 2k, \cdots \
     0, otherwise \end{cases}$
10. Difference in frequency : $nx[n] \leftrightarrow j\frac{d}{d\omega}X(e^{j\omega})$
11. Parseval’s Theorem : $\displaystyle \sum_{n=-\infty}^{\infty}|x[n]|^2 = \frac{1}{2\pi}\int_{2\pi}|X(e^{j\omega})|^2d\omega$
12. Convolution : $x[n]*h[n] \leftrightarrow X(e^{j\omega})H(e^{j\omega})$
13. Multiplication : $x[n]h[n] \leftrightarrow \frac{1}{2\pi}\int_{2\pi}X_1(e^{j\theta})X_2(e^{j(\omega - \theta)})d\theta$ (Periodic convolution)
14. Duality :

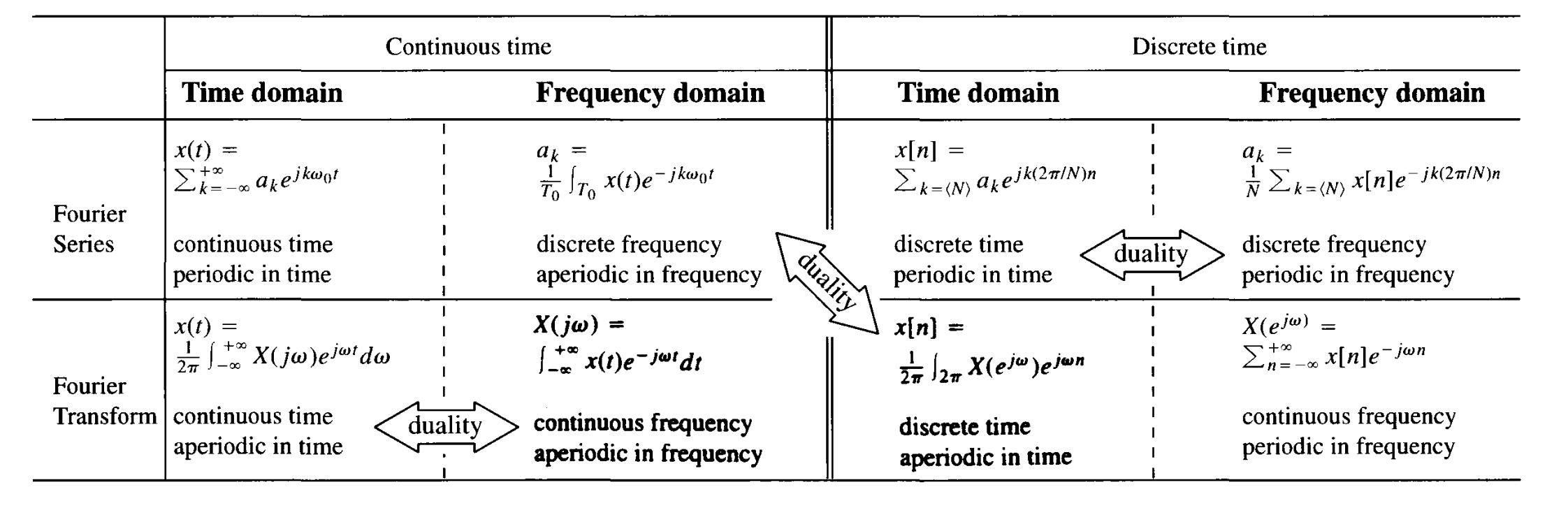
Chapter 6: Time and Frequency Characterization of Signal and Systems

这一章不知道在讲什么，好像考试也不是重点，随便整理一点

1. Magnitude and Phase of the Fourier Transform
   • Discrete FT:
     • $X(e^{j\omega}) = \displaystyle \left\vert X(e^{j\omega}) \right\vert e^{j\theta(\omega)}$
   • Continuous FT:
     • $X(j\omega) = \displaystyle \left\vert X(j\omega) \right\vert e^{j\theta(\omega)}$
   • $|X| = \displaystyle \sqrt{Re[X]^2+Im[X]^2}$
   • $\theta(\omega) = \displaystyle tan^{-1}\frac{Im[X(j\omega)]}{Re[X(j\omega)]}$
2. For LTI system: $H(j\omega) = \displaystyle \left\vert H(j\omega) \right\vert e^{j\theta(\omega)}$
   • $\left\vert H(j\omega) \right\vert $: Gain of the system
   • $\theta(\omega)$: Phase shift of the system
     • Linear phase system: $\theta(\omega) = -\omega t_0$
       • Linear phase system means a time shift of the input signal
     • Nonlinear phase system: $\theta(\omega) = \theta_0(\omega) - \omega t_0$
       • Nonlinear phase system means different frequency of the input signal has different phase change
3. Group Delay: $\tau_g(\omega) = -\frac{d\theta(\omega)}{d\omega}$
4. Bold’s Plot: Plots of $20\log_{10}\left\vert H(j\omega) \right\vert$ vs $\omega$ or $20\log_{10}\left\vert H(e^{j\omega}) \right\vert$ vs $\log_{10}\omega$
5. Step response of Ideal low-pass filters
   • $s(0) = \frac{1}{2}$,$s(\infty)=1$

Chapter 9: The Laplace Transform

1.Definition

• Laplace Transform: $X(s) = \displaystyle \int_{-\infty}^{\infty}x(t)e^{-st}dt$
• Laplace Transform pairs:
  • 
• ROC’s Properties:
  1. The ROC of $X(s)$ is a strip in the $s$-plane that contains the $j\omega$-axis
  2. If $x(t)$ is of finite duration and is absolutely integrable, then the ROC is the entire $s$-plane.
  3. If $x(t)$ is right-sided, and if the line $Re{s}=\sigma _0$ is in the ROC, then all values of $s$ for which $Re[s]>\sigma _0$ are also in the ROC.
  4. If $x(t)$ is left-sided, and if the line $Re{s}=\sigma _0$ is in the ROC, then all values of $s$ for which $Re[s]<\sigma _0$ are also in the ROC.

2.Properties

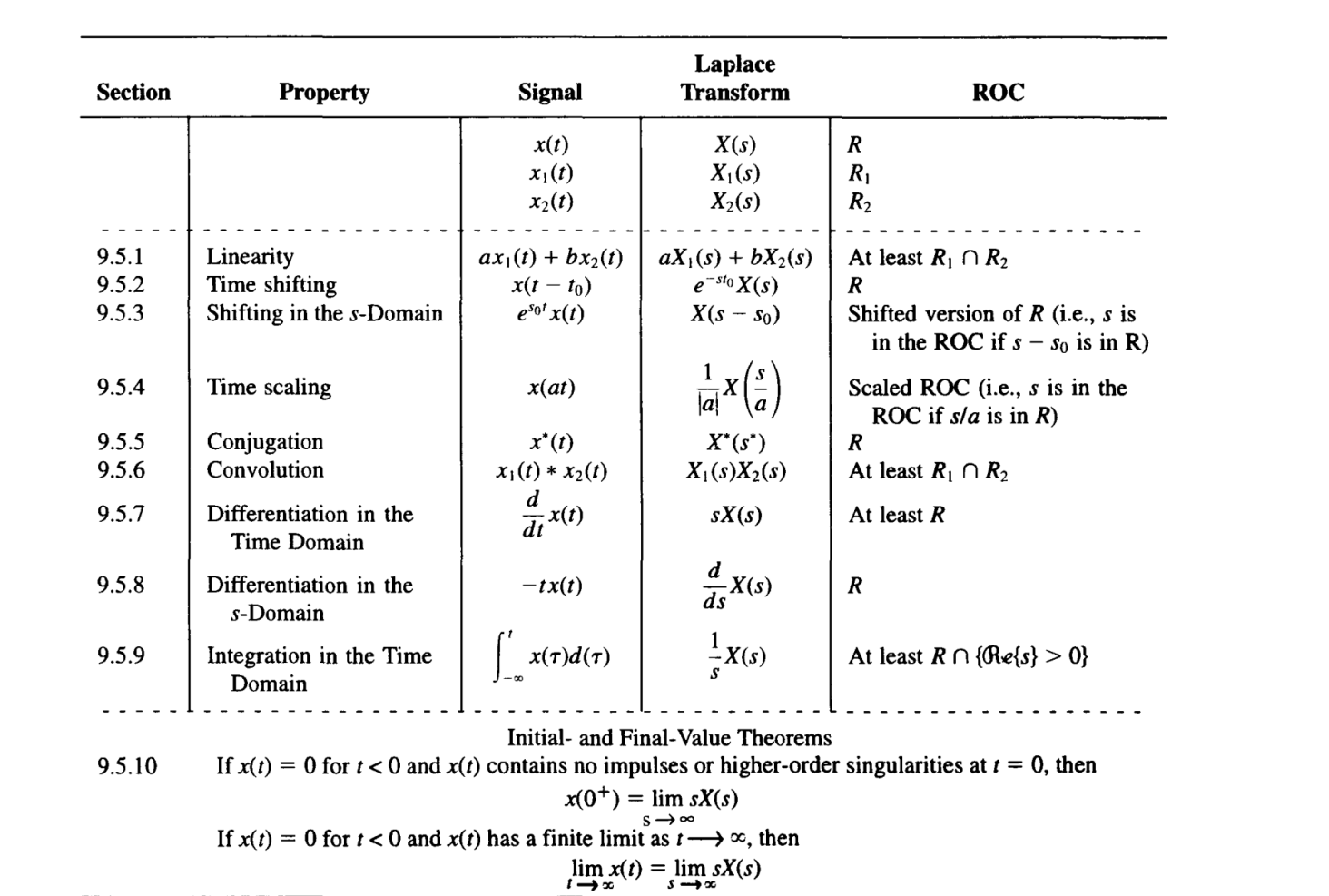
• Initial Value Theorem: If $x(t)=0$ for $t<0$,then $x(0^+) = \displaystyle \lim_{s\rightarrow \infty}sX(s)$

• Final Value Theorem: If $x(t)=0$ for $t<0$, $x(t)$ has a finite limit as $t\to \infty$, then $x(\infty) = \displaystyle \lim_{s\rightarrow 0}sX(s)$

3. LTI systems analysis using the Laplace Transform

1. Causal: ROC of $H(s)$ is the right half of the $s$-plane
   • A system with rational $H(s)$ is causal $\Rightarrow$ ROC of $H(s)$ is the right half of the $s$-plane
2. Stability: ROC of $H(s)$ includes the $j\omega$-axis
   • For a causal system: All the poles of $H(s)$ lie in the left half of the $s$-plane
   • All the poles have negative real parts

4. The unilateral Laplace Transform

• Differentiation in the time domain:
  • $\frac{d}{dt}x(t) \Leftrightarrow sX(s)-x(0^-)$
  • $\frac{d^2x(t)}{dt^2} \Leftrightarrow s^2X(s)-sx(0^-)-x’(0^-)$

Chapter 10: Z-Transform

1.Definition

• Z-Transform: $X(z) = \displaystyle \sum_{n=-\infty}^{\infty}x[n]z^{-n}$
• Z-Transform pairs:
  • 
• ROC’s Properties:
  • 1. The ROC of $X(z)$ is a ring in the $z$-plane that contains the unit circle
  • 2. The ROC of $X(z)$ doesn’t contain any poles of $X(z)$
  • 3. If $x[n]$ is of finite duration,then the ROC is the entire z-plane except possibly $z=0$ and $z=\infty$

2.Properties

3. LTI systems analysis using the Z-Transform

• Shifting Properties
  • $x[n-1] \leftrightarrow z^{-1}X(z)+x[-1]$
  • $x[n+1] \leftrightarrow zX(z)zx[0]$
  • $x[n-2] \leftrightarrow z^{-2}X(z)+z^{-1}x[-1]+x[-2]$